1.- Opciones para equilibrar el sistema

Para poder equilibrar el sistema que tenemos, lo que tenemos es cambiar de posición las cargas los apoyos y por tanto las distancias
que se encuentran en la viga, para que al final los momentos que tengamos sean del mismo valor y esto significara que esta en equilibrio.
2.- Calcular las reacciones.
Lo primero que se tiene que hacer es sacar los momentos
Para las 2T que tenemos uniformemente repartidas e
n una sección es necesario sacar la distancia, con el teorema de pitagoras
Que es igual a raíz de (4)al cuadrado + (4) al cuadrado que es igual a 5.6568
Después para calculo de momentos:
ΣMA= -11.3(2)-25(4)-R2(10)+43.3(4)+120= -22.6-100+10R20173.2+120
= -10R2+170=0
R2=-170/-10
R2=17
ΣFy=11.3+25+17=R1y+10
R1y=43.3
ΣFx=43.3=R1x
R1=61
3.- ¿Cuál es el esfuerzo en el cable y en la barra?
El tensor forma un triangulo y para sacar los valores es necesario :Cos40= 17.6 sobre la hipotenusa
Hip= 17.6 sobre cos40
Resultante=22.97

sen60º=pq/10 op=10sen60 pq=8.6= Ax
cos60º=ad/10
ad=10cos60
ad=5=Ay
cos45º=5/Hip
Hip=5/cos45

4.- ¿Cuál es el cortante y el momento del edificio?
Para graficar es necesario tener en equilibrio este sistema, lo que podemos notar es que esta empotrado así que para resolverlo debemos de tener una fuerza contraria al empotramiento o
sea contrario a las manecillas del reloj
El cortante en la base es igual a 8T ,
El momento osea la fuerza que debe de contrarrestar es de 36T
/ml

En el método de los nodos se tienen que contrarrestar las fuerzas en las barras para formar un equilibrio en este sistema, ya sea si suben 2 bajan dos o si bajan 4 suben 4, etc.
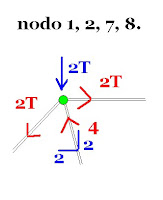


Por conveniencia y para no confundir se dice: Cuando la fuerza comprime al nodo el miembro esta en compresión. Cuando la fuerza sale del nodo el miembro esta en tracción.
